XYLENE POWER LTD.

FNR TEMPERATURE SETPOINT

By Charles Rhodes, P.Eng., Ph.D.

FNR TEMPERATURE SETPOINT:
This web page is primarily concerned with issues related to the FNR no load temperature setpoint To.
 

A FNR differs from water cooled reactors in that in a FNR the reactivity R is a well defined function of temperature T. The setpoint temperature To is the value of T at which R = 0.

At R = 0 the reactor design ensures that:
(dR / dT) < 0
which causes the nuclear process to passively maintain the average fuel temperature:
T = To.

The temperature setpoint To is primarily a function of the reactor fuel, coolant and fuel bundle properties and fuel structural geometry.

A practical concern in liquid sodium cooled reactors is that near the boiling point of liquid sodium the thermal coefficient of expansion of liquid sodium increases. This increase might be sufficient to change the sign of (dR / dT) which could cause a prompt critical accident. The liquid sodium would boil which would blow the fuel assembly apart. To prevent that happening it is essential to:
a) Keep the reactor setpoint temperature To far below the boiling point of liquid sodium;
b) To ensure that there is no local loss of liquid sodium coolant flow by ensuring that there are no hot spots in the sodium coolant which might allow the local temperature to rise toward the boiling point of liquid sodium;
c) To operate with a sufficiently negative value of [dR / dT] such that even if the sodium locally boils the local value of [dR / dT] remains negative. This object is most easily achieved by using Pu-239 instead of U-235 as the fission fuel to take advantage of the high TCE of plutonium.

One method of raising the boiling point of liquid sodium in the core zone is to keep a head of almost 10 m of liquid sodium above the core zone, which raises the sodium boiling point in the reactor core zone.

Another method is to monitor the temperzture everywhere in the core zone with sufficient resolution to detect any hot spots. This method involves scanning the core zone to find T as a function of position. At steady state :
T ~ To, so in effect this method finds To as a function of position in the core zone.

The object is to periodically adjust the movable fuel bundle insertions so that in each reactor movable fuel bundle:
T = To.

A key issue in FNR safety is to design the fuel bundles so that each fuel tube is cooled by multiple adjacent fuel channels. Blocked fuel channels will create a local hot spot and a local reduction in gamma output. Thus the combination of a higher discharge temperature and a lower gamma output than other fuel bundles may be indicative of a problem.
 

FNR TEMPERATURE SETPOINT To:
The fissile fuel of a FNR spontaneously maintains a average fuel temperature:
T = To
where To is known as the FNR's temperature setpoint. Typically this setpoint is fixed.

The temperature setpoint To is a function of the FNR's nuclear fuel geometry. For practical reasons To is typically chosen to be:
To = 460 degrees C.

These reasons include:
a) Ability to tolerate long term reactor operation with two adjacent sodium cooling channel blockages which at full load can cause the local peak fuel temperature to go as high as 560 degrees C;
b) Keeping the peak temperature of the interior stainless steel cup which forms the sodium pool liner under 475 degrees C, at which temperature long term stainless steel phase changes commence.
c) Protection of gaskets in Intermediate heat exchange bundles and NaK piping.
d) Prevention of fuel rod center line melting.

The balance of this web page is primarily concerned about peak fuel centerline temperature issues.

At average fuel temperature:
T = To
the FNR reactivity R is:
R = 0

As shown on the webpage titled: FNR REACTIVITY a requirement for FNR stablity is:
(dR / dT) < 0
at all accessible values of To.

The web page titled: FNR NATURAL SODIUM FLOW develops the relationship between (Tsd - Tsi), core zone sodium mass flow and FNR thermal power P, where:
Tsd = fuel assembly sodium discharge temperature
and
Tsi = fuel assembly sodium inlet temperature
 

FNR DESIGN:
At the operating point of a FNR:
(fission heating) = (thermal load)
and the average core zone fuel temperature of the FNR remains nearly constant at its temperature setpoint To.

At the FNR operating point the fission heat output must follow the relatively slowly varying thermal load. This load following requires that the number of free neutrons N in the FNR varies with the thermal load. If the thermal load falls to zero the fission heating must also fall to zero which means that N must also fall to zero.

Recall that the web page FNR Reactivity gave the number of free neutrons N in a FNR as:
N = No Exp[R (t - to)]
where:
No = number of free neutrons in the FNR at time:
t = to
and
R = FNR reactivity

This for the FNR to function as outlined above:
If T > To then:
R < 0
and
if T < To
then:
R > 0.

This condition is realized in FNR design by making reactivity R satisfy:
[R|T = To] = 0
and
[dR / dT] < 0
for all accessible values of To.

That condition is realized by choice of suitable FNR geometry while taking into consideration the known thermal coefficients of expansion of the various FNR materials. The temperature setpoint To is adjusted by using a mechanical arrangement to make a small change to the FNR fuel geometry.

Then at:
To = 460 degrees C
R = 0
and
[dR / dT] < 0
which is the requirement for a stable FNR.

There are practical limits on the size of [dR / dT]. It is essential that the inequality
[dR / dT] < 0
remain satisfied over the entire range of possible FNR fissile fuel concentrations and fuel geometries. It is also essential that if To is adjusted that T follow it. Any increases in setpoint To should be made under low load conditions.
 

AVERAGE FUEL TEMPERATURE MAINTENANCE IN A FNR:
Consider a thermally controlled FNR operating at its temperature setpoint To. Its thermal load is constant. Its reactivity R is zero.

If part of that FNR is then further cooled by a fluid coolant thermal contraction increases the concentration of fissile atoms in the cooled portion of the FNR fuel. That contraction causes the FNR reactivity R to become greater than zero, thus causing a rapid growth in the number of free neutrons N. Provided that the fuel rod length is not so large as to prevent sharing of fission neutrons, this phenomena enables relatively uniform heat production in the fuel rod and smooth coolant temperature rise as it flows along the length of the fuel rod.
The additional free neutrons quickly spread through the entire FNR and cause additional fissioning in uncooled regions of the FNR. The additional fissioning causes the temperature of the uncooled fuel regions to rise sufficiently above the average temperature setpoint To to reduce the FNR net reactivity R back to zero.

Thus a thermally controlled FNR has the remarkable property that, subject to geometric stability of its fuel assembly, it produces free neutrons which cause fission heating that maintains the FNR average fuel temperature at To independent of the thermal load. If one part of FNR fuel is fluid cooled then another part of the fuel warms up to keep the average FNR fuel temperature T constant at T = To.

The FNR temperature setpoint To is a function of the FNR fuel geometry. A FNR is designed so that at all accessible values of To:
[dR / dT] < 0.

The reactivity R increases with increasing fissile atom concentration. However, due to fuel thermal expansion the fissile atom concentration decreases with increasing fuel temperature, causing:
{[dR / dT]|T = To} < 0
which causes:
[dTo / dT] < 0.

This feature gives the FNR power and temperature stability. When:
T < To
then:
R > 0
and the production of free neutrons causes fission heating which causes the FNR average temperature T to spontaneously rise.

When the temperature T reaches To:
T = To
and
R = 0
net heating stops and the FNR temperature cannot further rise because:
[dTo / dT] < 0

If:
T > To
then:
R < 0
which causes N to rapidly fall to zero which stops further fission heating. If there is a thermal load there is a net loss of heat from the FNR and the average FNR fuel temperature will fall to:
T = To
before fission heating can restart.
 

A FNR normally operates such that when the sodium inlet temperature equals the FNR setpoint temperature To the rate of free neutron generation exactly equals the rate of free neutron loss so that the FNR thermal power is constant. If the sodium inlet temperature decreases then N increases causing the reactor thermal power to increase and if the sodium inlet temperature increases then N decreases and the reactor thermal power decreases.
 

FNR NO LOAD OPERATION:
Suppose that we consider a round core fuel rod of uniform radius and uniform fissionable material within a FNR.
At no load the fuel rod centerline temperature, the fuel rod surface temperature and the sodium temperature are all at To. At every point along the fuel rod there is a 0 degree C temperature difference between the fuel rod center line and the liquid sodium.
 

If the fuel rod material and the sodium coolant are initially all at
T = To = 460 degrees C = the FNR temperature setpoint,
the reactivity R = 0, there is no fission and hence the fuel rod emits no heat. This is the no load situation in a FNR.
 

UNIFORM HEAT LOADING:
Now assume that the outside surface of this fuel rod is uniformly cooled to:
(To - 25 degrees C).
The center line temperature of the fuel rod will instantly rise to (To + 25 degrees C) to keep the average fuel rod temperature Ta constant at:
Ta = To.
At full load there is a 50 degree C temperature difference between the fuel rod center line and the fuel rod outside surface which will cause an ongoing radial heat flow from the fuel through the fuel rod outside surface, through the fuel tube and into the coolant.

Now assume as shown at _____that at full load (1 GWt the temperature drop across the fuel tube wall is 10 degrees C.

Now assume that coolant sodium flows parallel to the fuel rod surface confined by cooling channels. The inlet sodium cools the fuel tube and hence the outside surface of the fuel rods. The cooling sodium flows parallel to the fuel rods absorbing heat. Assume that the sodium flow rate is chosen such that the sodium gains temperature with vertical distance at the same rate as does the outside surface temperature of the fuel rod. This situation results in uniform thermal loading of the fuel rod.

Assume that at full load at the sodium inlet end of the fuel rod the flowing sodium coolant causes the outside surface of the fuel rod to be further cooled by 20 degrees C from:
(To - 25 degrees C)
to:
(To - 25 degrees C - 20 C).

At ________ it is shown that with a 1 GWt thermal load the temperature drop across the fuel rod radius is 50 degrees C.

At FNR Natural Sodium Flow it is shown that with our fuel geometry a 1 GWt load corresponds to a 40 degree C axial temperature drop through the flowing liquid sodium.

Then to maintain the fuel rod average temperature:
Ta = To:
the fuel rod outside surface temperature at the sodium discharge end of the fuel rod will rise to:
(To - 25 degrees C + 20 degrees C).

Now at the fuel rod position equidistant from the ends of the fuel rod the average fuel rod temperature is Ta = To, the fuel rod surface temperature is:
(To - 25 degrees C)
and the fuel rod centerline temperature is:
(To + 25 degrees C).

At full load the fuel rod centerline temperature varies from:
(To - 25 degrees C - 20 + 50 degrees C))(
at the sodium inlet end to
(To - 25 degrees C + 20 + 50 degrees C)
at the sodium discharge end.
 

NORMAL FULL LOAD OPERATION:
Now assume that as shown at ________ that at full load there is a 10 degree C temperature drop across the fuel tube wall. Hence at full load the temperature in the flowing liquid sodium varies from:
(To - 25 degrees C - 20 - 10 degrees C) = (To - 55 C)
to:
(To - 25 degrees C + 20 - 10 degrees C) = (To - 15 C)
 

TEMPERATURE DROP WITH LOAD:
Note that at no load the sodium discharge temperature is:
To
and at full load the sodium discharge temperature is:
(To - 15 degrees C).

Note that at no load the sodium inlet temperature is:
To
while at full load the sodium inlet temperature is:
(To - 55 C)

Hence in normal full load operation the maximum fuel center line temperature is:
(To - 15 degrees C) + 60 degrees C = To + 45 degrees C
and the minimum fuel centerline temperature is:
(To - 55 degrees C + 60 degrees C) = (To + 5 degrees C)
 

EFFECT OF INTERMEDIATE HEAT EXCHANGE BUNDLE:
Assume that the full load temperature drop across the intermediate heat exchange bundle is 10 degrees C.
Thus there is a significant issue that at no load the NaK discharge temperature potentially rises to To whereas at full load the NaK discharge temperature drops to about:
(To - 15 degrees C - 10 degrees C) = (To - 25 degrees C).
 

EFFECT OF NaK/nitrate salt HEAT EXCHANGER:
Assume that there is a further 10 degree C temperature drop across the NaK/nitrate salt heat exchanger. Then the highest possible nitrate salt discharge temperature at full load conditions is:
(To - 35 degrees C)
 

BLOCKED COOLING CHANNELS:
In the FNR discussed herein each fuel tube has associated with it four sodium cooling channels. If two of those channels are obstructed the fission heat generated in the fuel will remain unchanged but the sodium coolant flow will be reduced by a factor of two. Hence the sodium temperature rise along the length of the fuel rod will double but the radial temperature drop within the fuel rod will remain the same.

At full load as shown above the sodium inlet temperature is:
(To - 55 degrees C).
With blocked cooling channels for the affected channels the sodium temperature rise is:
2 X 40 degrees C = 80 degrees C
Hence for the affected cooling channels the sodium discharge temperature becomes:
(To - 55 degrees C + 80 degrees C = To + 25 degrees C
and the correponding fuel centerline temperature is:
(To + 25 degrees C + 60 degrees C) = (To + 85 degrees C)

For a 600 degree C maximum centerline temperature:
this formula sets the maximum value of To at:
(To + 85 degrees C) = 600 C
or
To = 515 degrees C
in which case the maximum value of the normal full load sodium discharge temperature is:
To - 15 degrees C
= 515 C - 15 C
= 500 C
 

BLOCKED COOLING CHANNEL + FUEL TUBE SWELLING:
Over the fuel tube operating life there will be some fuel tube swelling. The effect of this swelling is to reuce the cooling chanel cross section which will increase the sodium temperature rise. Assume that the axial temperature rise becomes 50 degrees C. Then in the blocked cooling chnnel case the temperature rise along a blocked channel becomes:
2 X 50 C = 100 C.

In normal full load operation with swollen fuel tubes:
Sodium inlet temperature = (To - 25 degrees C - 25 - 10 degrees C) = (To - 60 C)
to:
Sodium discharge temperature = (To - 25 degrees C + 25 - 10 degrees C) = (To - 10 C)

To avoid fuel centerline melting the highest value of To is given by:
(To + 100 C) = 600 C
or
To = 500 C

Thus the choices of To are:
To = 460 C to prevent gasket deteriortion
To = 475 C to prevent SS phase change
To = 500 C to prevent fuel rod center line melting

FNR NO LOAD OPERATION SUMMARY:
At no load the fuel rod centerline temperature, the fuel rod surface temperature and the sodium temperature are all at To. At every point along the fuel rod there is a 0 degree C temperature difference between the fuel rod center line and the liquid sodium.
 

FNR NORMAL FULL LOAD OPERATION SUMMARY:
At every point along the fuel rod there is a 60 degree C temperature difference between the fuel rod center line and the liquid sodium. Over the fuel rod length the sodium temperature rises from:
(To - 55 deg C) at the sodium inlet to:
To - 15 C

At full load the normal fuel rod centerline temperature rises from:
(To - 55 C + 60 C) = (To + 5 degree C)
to:
(To - 15 degree C + 60 deg C)
= (To + 45 deg C)

The absolute maximum value of To set by two adjacent blocked cooling chammels plus swellingis 500 degrees C
 

LOCAL TEMPERATURE RISE VARIATIONS:
A significant issue in FNRs is local variations in fuel rod temperature rise. In a FNR the concentration of free neutrons varies only slowly with position. However, the rate of heat generation in a core fuel rod is proportional to the product of the free neutron concentration and the fissile fuel atom concentration. Hence if core fuel rods in the same fuel bundle have significantly different fissile atom concentrations the heat output per fuel rod will be significantly different.

In a FNR with natural circulation of the sodium coolant an increased heat output per fuel rod due to a higher fissionable atom concentration causes an increase in liquid sodium flow past the fuel rod, so the change in sodium discharge temperature from fuel tube to fuel tube due to variations in fuel concentration is mitigated.

However, there is a potential complication that some sodium cooling channels might become partially obstructed as compared to other primary sodium cooling channels. Hence there can be significant local sodium discharge temperature variation resulting from sodium cooling channel obstruction. The effect of adjacent cooling channel cross section variations due to fuel tube warping tends to cancel. However, that is not the case if the cooling channel cross section variations are due to foreign particle obstruction.
 

BLOCKED COOLING CHANNEL STATISTICS:
Assume that during the life of the reactor due to unforeseeable causes the primary sodium acquires a few particulates that are capable of blocking FNR cooling channels. Assume that the reactor has 300,000 cooling channels and that the reactor is in nearly constant operation. The probability of the first particulate blocking some cooling channel somewhere is 100%. The probability of the second particulate blocking a cooling channel adjacent to the first blocked channel is (4 / 300,000). The probability of the 3rd particulate blocking a cooling channel adjacent to the first two cooling channels is (6 / 300,000). Hence 2 blocking size particulates will not force a FNR shutdown but 3 blocking sixe particulates hava a:
(4 / 300,000)(6 / 300,000) = (24 / 9 X 10^10) = 1 chance in 3.75 billion of forcing a reactor shutdown.

Clearly it is important to do all necessary to minimize the number of potentially cooling channel size blocking particles that get into the sodium pool. It may also necessary to provide a filter with every active fuel bundle. The filter must stop potentially blocking particles but must not introduce significant flow resistance.
 

FINE ADJUSTMENT OF To:
The set point To is dependent on the FNR fissile fuel atom concentration and on the fuel geometry. The setpoint temperature To can be changed by changing the fuel geometry.

During normal FNR operation, over a period of years, the FNR temperature set point To will gradually decrease due the long term changes in the FNR fissile fuel atom concentration. In order to keep
To = constant
it is necessary to occasionally make small changes in the fuel geometry. These changes are achieved by small increases in the insertion of movable fuel bundles into the matrix of fixed fuel bundles.
 

GROSS ADJUSTMENT OF To
From time to time a FNR shutdown may be necessary to permit FNR refuelling and / or to replace an intermediate heat exchange bundle. In those circumstances a FNR cool shutdown is executed which means that To is reduced to:
To = 120 degrees C
which is a low enough temperature to permit robotic work in the sodium pool enclosure while still being hot enough to prevent the liquid sodium from changing from its liquid to its solid state. When the reactor temperature T approaches 120 degrees C the reactor thermal load should be set to match the thermal power from fission product decay heat. Then the reactor should be left for about one week to allow natural decay of Na-24 in the primary sodium pool. Only then can robotic work in the sodium pool enclosure commence.

The set point temperature To is changed by changing the reactor fuel geometry. The set point temperature To is only reduced when it is necessary to lower the temperature of the sodium pool.
 

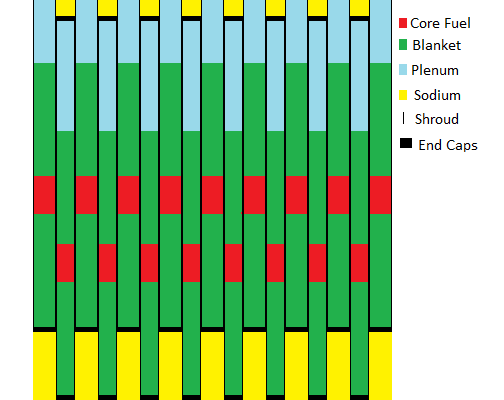
FUEL BUNDLE STATE DIAGRAM:
The insertion positions for a line of 8 movable fuel bundles inserted between 9 fixed fuel bundles are shown below for the cases of reactor cold shutdown, normal reactor operation and reactor at maximum possible power. In the reactor cold shutdown state the core rods (red) form two widely separated upper and lower core rod fuel concentration layers. In the normal reactor operating state the fixed and movable core rods partially overlap forming the core zone. As the fuel ages the amount of core rod overlap is gradually increased which increases the thickness of the core zone. When the fixed and movable core rods fully overlap the fuel bundles are ready to be removed for fission product decay cooling and then removal and reprocessing.
 

Reactor Cool Shutdown

 

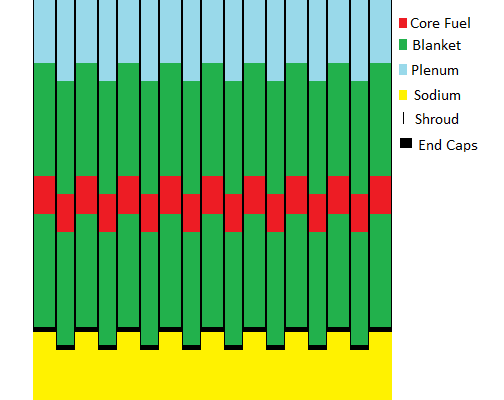Normal Reactor Operation

 

Reactor at Maximum Movable Fuel Bundle Insertion
 

Note that the maximum permitted vertical travel of a movable fuel bundle is 1.1 m which causes the transition between the movable fuel bundles fully withdrawn (reactor cold shut down) and movable fuel bundles fully inserted (maximum thermal power) states. Note that rapid over insertion of the movable fuel bundles into the matrix of fixed fuel bundles could potentially cause prompt neutron criticality.
 

FNR WARMUP:
When the work within the sodium pool enclosure is complete the set point temperature To can be slowly raised back to its normal value of:
To .

Define:
Tpi = FNR fuel bundle primary sodium inlet temperature

For a reactor intended to operate with:
(To - Tpi) < 50 degrees C
it is important on reactor warmup to slowly raise the fuel temperature setpoint To to gradually raise the temperature Tpi in the sodium pool so that the difference between To and Tpi never exceeds 50 degrees C.

It is easy to damage a FNR during sodium pool warm up by increasing To too quickly. After a movable fuel bundle step insetion the liquid sodium surface temperature as a function of time should plateau before the movable fuel bundle insertion depth is further increased.

During FNR warmup the moveable fuel bundles must be very slowly inserted into the matrix of fixed fuel bundles with no external thermal load to ensure that the peak fuel centerline temperature rating is not exceeded. This issue is particularly important when the fuel is new so the movable fuel bundle insertion distance is small which means that the available heat dissipation area on the core fuel tubes is minimum.

In a practical FNR the large sodium pool should prevent a rapid change in temperature T. However, a practical FNR relies on an upper limit to the NaK flow rate to prevent (To - T) in the sodium exceeding its maximum rated value.
 

PROTECTION AGAINST A DEFECTIVE CONTROL SYSTEM:
In the event that due to a control system malfunction a new movable fuel bundle is erroneously driven toward its fully inserted state it is essential for the other movable fuel bundles, which are separately controlled, to immediately fully withdraw to cause a reactor cool shutdown.

When the fuel is new (average 20% Pu) and every second movable active fuel bundle is at its normal insertion depth while the remaining movable active fuel bundles are fully withdrawn the chain reaction must stop. This condition ensures that a cool shutdown condition is attainable with any one movable fuel bundle jammed in its normal operating position.

It is important to ensure that one isolated movable active fuel bundle with new fuel will not go prompt critical if it is accidentally fully inserted into the fixed fuel bundle matrix. As this circumstance is occurring the other independent shutdown system must instantly force a reactor cool shutdown. That cool shutdown will cause the four nearest neighbour movable fuel bundles to immediately fully withdraw. Hence, in all fuel conditions reactor prompt neutron criticality must be impossible if the four nearest neighbour movable active fuel bundles are fully withdrawn.

For clarity if the fixed fuel bundles are designated by Fx and the interlaced movable fuel bundles M are grouped by a, b then in plan view:
Fx = Fixed core fuel bundle
Ma = Movable coe fuel bundle group a
Mb = Movable core fuel bundle group b

ROW	FUEL BUNDLE TYPE
1	Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma
2	Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx
3	Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma Fx Ma
4	Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx Mb Fx

Note that each fixed fuel bundle Fx is surrounded by 2 X Ma and 2 X Mb with 4 fixed bundles Fx on diagonals (except for the outer perimeter).
Note that each type a movable bundle is surrounded by 4 X Fx fixed bundles with 4 X Mb movable bundles on diagonals (except for the outer perimeter);
Note that each type b movable bundle is surrounded by 4 X Fx fixed bundles with 4 X Ma movable bundles on diagonals (except for the outer perimeter).

Note that Ma and Mb movable bundles occur in every second row and every second column.

Thus if any Ma bundle jams the four nearest Mb bundles should be withdrawn to compensate. Similarly if any Mb bundle jams the four nearest Ma bundles should be withdrawn to compensate.

Achieving certain reactor shutdown while allowing for the desired range of Pu-239 concentration decay in the core fuel rods likely requires a 1.1 m movable fuel bundle withdrawal. A 1.8 m blanket thickness is required to guarantee 1.2 m blanket thickness at times when there is almost no overlap between the fixed and movable core fuel rods. More typically the fuel bundle core rod overlap is about 0.45 m resulting in a guaranteed 1.65 m blanket thickness.
 

THERMAL POWER:
The web page titled:FNR NATURAL SODIUM FLOW develops the relationship between (Tsd - Tsi) and FNR thermal power P. It is shown on this web page that normally:
Tsd ~ To

The thermal resistance related to the fuel rods and fuel tubes in a FNR causes the FNR sodium discharge temperature Tsd at full load to be 60 degrees C less than the peak fuel rod center line temperature Tch at the hot end of the fuel rod. The temperature difference:
(Tch - Tsd)
increases with reactor thermal power. The thermal resistance is the combined effect of the finite thermal conductivities of the fuel rod, the sodium internal to the fuel tubes, the fuel tube wall and the sodium coolant boundary layer on the outside of the fuel tube wall.

However, the reactor thermal power P can also be expressed in terms of the coolant temperature rise in the form:
P = Fs Cp (Tsd - Tsi)
where:
Fs = sodium mass flow rate through the core zone;
and
Cp = sodium heat capacity.

The import of this equation is that if there is a high sodium coolant flow rate Fs, the temperature differential:
(Tsd - Tsi)
may have to be reduced to prevent the FNR's heating element thermal power rating being exceeded.

For a FNR which relies on natural sodium circulation this relationship indirectly sets the required number of active fuel tubes corresponding to a particular sodium flow rate and temperature differential.
 

Note that as the sodium flow rate Fs goes to zero then P goes to zero.

In the practical FNR described herein the NaK flow rate Fs is controlled to limit the FNR thermal power. Hence the FNR converges to a steady state condition where the fission thermal power output equals the rate at which heat is removed by the NaK coolant.
 

As shown on the web page FNR NATURAL SODIUM FLOW, in order to have sufficient sodium natural circulation at full thermal power we want to operate at:
P = 1000 MWt at:
Tsd = 460 C,
Tsi = 420 C

WARNING:
Historically in other liquid sodium cooled reactors there have been a number of cases of FNR fuel centerline melting. It is important to realize that the nuclear reaction will deliver the instantaneous thermal power:
P = Fs Cp (Tsd - Tsi)
where:
Tsd = sodium discharge temperature from core fuel tubes
Tsi = sodium inlet temperature to core fuel tubes

This thermal power is delivered by thermal conduction from the nuclear fuel througn the fuel tube walls and into the liquid sodium. The nuclear reaction is unaware that thermal power P can easily physically exceed the available thermal conduction heat transport capacity, thus causing fuel center line melting.

The sodium flow through the FNR core zone will typically be ~ 2X the total NaK flow. Thus IT IS ESSENTIAL TO ENSURE GOOD MIXING OF THE COOL SODIUM BEFORE IT REACHES THE BOTTOM OF THE FUEL ASSEMBLY.

It is up to the FNR system designer to do all necessary to keep the thermal power P within the FNR's physical material limits. A simple way to achieve that objective in normal FNR operation is to limit the the thermal power that can flow through the FNR's NaK heat transport loops. However, care must still be used during FNR warmup.

In simple language the nuclear reaction in a FNR supplies sufficient instantaneous thermal power to discharge sodium at set point temperature To, irrespective of FNR material related heat transport limitations. If the system designer fails to do all necessary to limit the maximum value of:
P = Fs Cp (Tsd - Tsi)
or if reactor operators and/or service personnel defeat mechanisms designed to limit the maximum rate of change of:
To
sooner or later the FNR heat transport capacity will be exceeded and the fuel may be damaged.
 

SOURCE OF HISTORICAL FNR PROBLEMS:
Suppose that a historical FNR for some reason was shut down using its control rods. While in the off state the sodium pool gradually cooled. When the reactor was to be used again the control rods should have been withdrawn very slowly to gradually bring the sodium pool back to its design operating temperature. Too rapid withdrawal of the control rods would cause a FNR thermal power surge sufficient to damage the FNR fuel and/or fuel tubes.
 

OPERATING SUMMARY:
The FNR thermal power is proportional to both the coolant flow rate Fs and
(Tsd - Tsi).
A FNR spontaneously varies its thermal power output to maintain a constant average fuel temperature To, where: To ~ Tsd.
Flow rate Fs is a natural circulation flow rate which is a function of (Tsd - Tsi).

In normal opertion reactor power P is limited by the heat transport rate through the NaK heat transport loops which rate is established by induction pumps. In the event of loss of station power the induction pumps will not operate, but the NaK loops should provide enough natural circulation for removal of fission product decay heat.
 

The NaK temperature and flow sets the steady state thermal power that the FNR must supply. For each value of To = Tsd and Tsi there is a corresponding value of Fs and hence a corresponding thermal power. In supplying that thermal power we must ensure that the temperatures stay within their rated range.
 

This web page last updated on March 1, 2024.

Home	Energy Physics	Nuclear Power	Electricity	Climate Change	Lighting Control	Contacts	Links